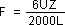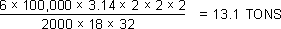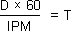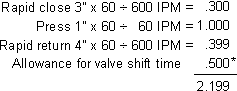Formulas and Data
How to compute tonnage requirements:
- General - When pressure per square inch is known:
psi x area of work/2000 = 2 tons of ram force required
Example: Where it is known that 100 psi is needed to do a job on a 5" x 8" wide piece.
100 x 5" x 8"/2000 = 2 tons
- Press Fit - To determine the force required to press fit two round pieces together such as a shaft pressed into a bushing, use the following formula:
F = D x ϖ x L x I x P/2
Where:
F = force required in tons
D = diameter of the part to be pressed in inches
L = length of part to be pressed in inches (Note: the length of the interference fit only.)
I = interference in inches (usually .002" to .006")
P = pressure factor (See table below).
| Diameter (inches) | Pressure Factor | Diameter (inches) | Pressure Factor | Diameter (inches) | Pressure Factor | Diameter (inches) | Pressure Factor |
| 1 | 500 | 3 | 156 | 5 | 91 | 7 | 64 |
| 1¼ | 395 | 3¼ | 143 | 5¼ | 86 | 7¼ | 61 |
| 1½ | 325 | 3½ | 132 | 5½ | 82 | 7½ | 59 |
| 1¾ | 276 | 3¾ | 123 | 5¾ | 78 | 7¾ | 57 |
| |
| 2 | 240 | 4 | 115 | 6 | 75 | 8 | 55 |
| 2¼ | 212 | 4¼ | 108 | 6¼ | 72 | | |
| 2½ | 189 | 4½ | 101 | 6½ | 69 | | |
| 2¾ | 171 | 4¾ | 96 | 6¾ | 66 | | |
Example: A steel shaft 2" in diameter pressed into a hole 3" long. The interference fit between the two diameters is .006".
2" x 3.14 x 3" x .006" x (240/2) = 13.56 tons
- Punching - A quick guide to determine tonnage requirements for punching steel is:
Diameter x thickness x 80 = tons (where 80 is constant for steel. Use 65 for brass.)
Example: A 3" hole in .250" stock: 3" x .250" x 80 = 60 tons
For noncircular holes, instead of the diameter, use 1/3 of the total length of cut.
Example: A rectangular hole 4" x 6" in .250" stock: (4" + 6" + 4" + 6"/3) x .250" x 80 = 133.3 tons
- Deep Drawing - Deep-drawing calculations can be complex. The press, dies, material, radius, and part shape all have bearing. For drawing round shells, the following formula is a simple guide:
C x T x Ts = tons
Where:
C = circumference of the finished part; T = material thickness in inches; and
Ts = tensile strength of the material.
Example: To draw a 5" diameter cup of .040" stock with a tensile strength of 46,000 psi would require the following tonnage:
(5 x 3.1416) x .040 x (46000/2000) = 14.44 tons
A 20-ton press would be recommended
- Straightening - The pressure required to straighten a piece of metal depends on its shape. Below is an approximate formula with a further definition for different shapes.
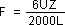
Where F is the ram force in tons; 6 is a constant; U is ultimate strength of the material in psi; Z is the section modulus (see below); and L is the distance between the straightening blocks in inches.

Example: A 2" diameter shaft, 18" between the blocks, 100,000 psi ultimate strength.
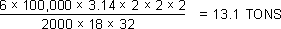
How to determine strokes per minute for a hydraulic press
The number of strokes per minute for a hydraulic press is determined by calculating a separate time for each phase of the ram stroke. The rapid advance time is calculated, then the pressing time, (the work stroke); then, if there is no dwell time, the rapid return.
The basic formula for determining the length of time in seconds for each phase of the stroke:
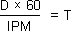
Example: a hydraulic press with a 600 IPM rapid advance, 60 IPM pressing speed, and 600 IPM rapid return. The work requires a 3" advance, 1" work stroke, and 4" rapid return.
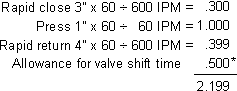
60 ÷ 2.199 = 27 cycles per minute.
* Electrical actuation and valve shift time varies depending on the type of hydraulic circuit. One half second is a reasonable average figure.
1. These formulae are intended as guidelines only. Please consult a qualified manufacturing engineer for recommendations concerning your specific requirements.
2. Based on steel shaft and cast iron bushing (with OD/ID > 2).
Next Section
|